First things first, this is just a great example of how to write crackmes/hackmes/whatevermes for learning, so thanks a lot for this opportunity!
And yes, it’s better to strip the binary, it’s much more interesting.
Phase 1
Answer: I am just a renegade hockey mom.
This is a simple string comparison, nothing special.
Phase 2
Answer: 1 2 4 8 16 32
The first number must be 1. The algorithm checks that the next number is 2n from the previous one, or something like that:
1 2 3 4 5 | for (int i = 1; i <= 6; ++i) { if (2*result[i-1] != result[i]) { boom(); } } |
Phase 3
Possible answers:
| Number1 | Number2 |
| 0 | 602 |
| 1 | -26 |
| 2 | 562 |
| 3 | -126 |
| 4 | 0 |
| 5 | -126 |
The first number must be <= 5. The second number depends on the first, the calculation is based on the switch with the fallthrough logic as follows:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | int result = 0; switch(num1) { case 0: result = 0x274; case 1: result -= 0x24C; case 2: result += 0x2B0; case 3: result -= 0x7E; case 4: result += 0x7E; case 5: result -= 0x7E; case 6: result += 0x7E; case 7: result -= 0x7E; break; default: boom(); |
Phase 4
Answer: 3 10
This is a fun algorithm that does a “binary search” on an array of numbers [0..14] and sums up the “middle” of each split. The question is what number the algorithm must find so that the sum of the midpoints of the partitions is 10.
1 2 3 4 5 6 7 8 9 10 11 12 13 | unsigned calculate(unsigned num, unsigned left, unsigned right) { unsigned result = left + (right-left) /2; if (result > num) { result += calculate(num, left, result-1); } else if (result < num) { result += calculate(num, result + 1, right); } return result; } if (calculate(number1, 0, 14) != 10) boom(); |
So when it looks for the number 3, the splits with midpoints will be:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14] [1, 2, 3, 4, 5, 6]
and the sum of midpoints is 10.
Phase 5
Answer: 5 115
The data structure used in this step is a type of circular linked list, where the value of the given index in the array is a pointer to the next element (i.e. the next index). This is the array in the binary:
[ 10, 2, 14, 7, 8, 12, 15, 11, 0, 4, 1, 13, 3, 9, 6, 5]
which results in the following linked list:
10->1->2->14->6->15->5->12->3->7->11->13->9->4->8->0->(10 which is the first element)
The task is to find the element from which the number of elements traversed to the endpoint (which is the element with value 15) equals 15. Given that there are 16 elements in the list, we need to start from the element pointed to by element 15, which is 5. This is the first number.
The second number is the sum of all the elements passed minus the element we started from. So it’s just (15*16)/2 - 5 which is 115.
Phase 6
Answer 5 4 3 1 6 2
The data structure in this problem is a true linked list with pointers, but it is built dynamically. Or, to be more precise, the list is already built in the binary, but the entered numbers reinitialize the links and build the list in the requested order.
Initially, the linked list looks like this:
{value=530, idx=1} -> {value=450, idx=2} -> {value=533, idx=3} -> {value=915, idx=4} -> {value=935, idx=5} -> {value=512, idx=6} -> null
The correct answer is a sequence of numbers that makes up a sorted list in descending order.
Secret phase
As a bonus, there is a secret phase that can be activated if you add the string “DrEvil” to the answer in step 4, so it should be “3 10 DrEvil”.
The data structure at this stage is a classic binary tree, and the problem to be solved is a variant of the “sum of paths” algorithm. In this case, in each direction you choose “costs” either 2n (left) or 2n+1 (right), where n is the current sum of all costs. So, for example, if you go to the right from the head, the sum will be 1. If you go to the right again, you will get 3 (21+1), to the left – 2 (21), and so on. The task is to find a path that will “cost” 5.
Here is the tree on which the algorithm works (thanks to binary-tree-visualizer for visualization):
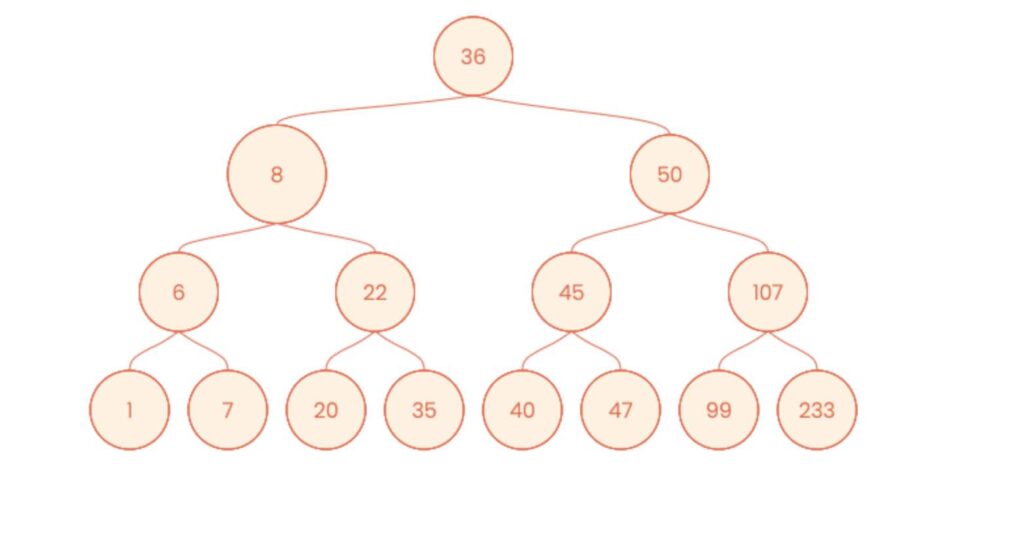
It’s probably worth writing tree traversal code that finds a path, but since the tree is small, it’s faster to do it on paper.
Answer 42, from my point of view, would be the perfect completion of the lab, but for some reason the answer is 47.
